What is the probability of having a particular amount of money in Stardew Valley? That’s the question asked by this Reddit post on r/StardewValley.

Screenshot of Reddit post (captioned in post) “Just casually playing then got a perfect $111,111” What are the odds of having exactly 111,111 gold during normal play?

The first thing to notice about this problem is that it’s determined by how you play the game. In Stardew Valley, you generally gain gold by selling items and lose gold by buying items. So, the amount of gold you have is some function of the items you have, the items you want, the items you can buy, and the gold you have.

To determine the probability of having a particular amount of money, we could attempt to model the changes to your gold amount by observing your play, but in my opinion that won’t lead to a very satisfying answer. Instead, I might like to reason in reverse: if I adopted a particular style of play, how likely is it that I would stumble onto a particular gold total? This approach ignores individual play differences and focuses on the likelihood of a particular gold total relative to other gold totals given assumptions about playstyle.

To answer the question, I’ll use a highly simplified play model:

  • The player never decreases their money total. In other words, we will ignore all player purchases e.g. seeds. Getting to a special number “from above” is less exciting than getting to it from below!
  • The player will only make money by selling the 30 crops for which the player can buy seeds from Pierre/JojaMart.
  • The player will sell crops one at a time. (In other words, the player doesn’t sell in bulk using the bin.)
  • The player is farming level 1 and doesn’t use fertilizer. (That means no Iridium-quality crops will appear.)
  • The player has access to a stockpile of all crops and will sell crops out of season.

Using this assumed playstyle, we can answer our original question by simulating games of Stardew Valley starting from 0g.

Simulating a game of Stardew Valley to 111,111g

To simulate a game of Stardew Valley, we first need to know how much money we can make from selling various crops. Fortunately, we can get that data from the Stardew Valley Wiki page for “Crops”.

Using Python pandas and lxml, getting the data is easy.

# you can call read_html() directly with the URL (https://stardewvalleywiki.com/Crops),
# but I downloaded a local version of the page so I know I'll have the same data if I run this later
with open("stardew_valley_wiki_crops.html") as infile:
    df_list = pd.read_html(infile)

df_list now contains 121 Pandas dataframes, corresponding to each of the HTML tables on the page (including tables nested inside other tables). By looking at a few of the tables in Jupyter notebook, I wrote some simple parsing code to pull out the prices for the three quality levels for each crop. Now we have data that looks like this:

Corn [50, 62, 75]
Hops [25, 31, 37]
Pepper [40, 50, 60]
Melon [250, 312, 375]
...

The last data we need to run simulations is the probability of the farmer harvesting a crop of each quality level. Based on the documentation on the wiki, we can compute those easily:

farming_level = 1
fertilizer_level = 0
gold_prob = 0.2 * (farming_level / 10) + 0.2 * (fertilizer_level) * ((farming_level + 2) / 12) + 0.01
silver_prob = gold_prob * 2
basic_prob = 1 - (gold_prob + silver_prob)

At farming level 1, our simulated player will harvest basic crops 91% of the time, silver crops 6% of the time, and gold crops 3% of the time.

We reshape the price data into a NumPy array so we can easily sample from it by selecting random indices.

# price array
prices.shape
(30, 3)

To do sampling, we’ll create a random number generator (RNG):

rng = np.random.default_rng(506275)

Then, to find out what the player will buy, we sample a random crop and a random quality:

def sample_player_sale():
    crop = rng.integers(0, 30)
    quality = rng.choice([0, 1, 2], p=[basic_prob, silver_prob, gold_prob])
    sale = prices[crop, quality]

A simulated game involves sampling sales until the player hits or exceeds the target value: 111,111g.

def simulate_game(target_value:int = 111111) -> bool:
    total_gold = 0
    while total_gold < target_value:
        sale = sample_player_sale()
        total_gold += sale
    did_hit_target_value = total_gold == target_value
    return did_hit_target_value

Implementation detail: to increase game simulation speed, we actually sample a large array of crops and qualities into memory and then iterate over those as sales.

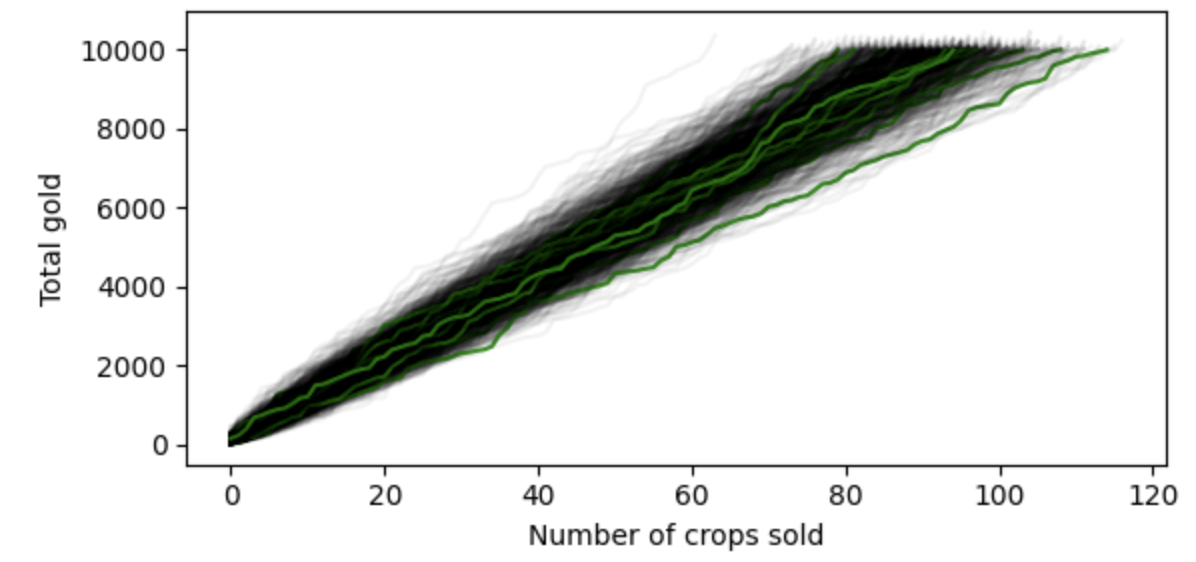10 different games to 1000g 1000 simulated games to >10,000g. Only a few will hit exactly 10,000g.

The figure above shows 1000 random games, but played to a target value of only 10,000g so we can see what’s going on. The green lines show games that hit exactly 10,000g, while the rest overshot. Over 1 million simulated games, the probability of a game hitting exactly 10,000g is 0.93%.

So how likely is the player to get exactly 111,111g?

From 10 million games simultated using our assumed playstyle, the player will hit exactly 111,111g in 0.92% of games.

That’s a pretty good answer, in my opinion! It suggests the Reddit user who inspired this really did have something unusual happen. A natural follow-up question to ask: is hitting 111,111g more or less likely than other similar values e.g. 100,000g, 111,100g, etc.?

We can use our 10 million simulated games to compute the same percentage for other values near our target value.

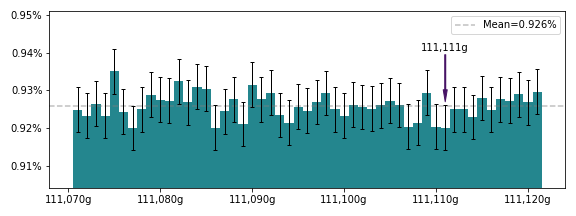Probability of exact gold values 111071-111121. No gold value is statistically distinguishable from the mean. Observed probability of achieving various gold amounts near 111,111g in 10 million simulated games.

We can definitely see some variance, but even with 10 million games those differences may be due to randomness introduced by our simulation. In fact, the error bars in the figure are Binomial confidence intervals at the 95% confidence level (computed via SciPy). None of the simulated probability estimates is significantly different from the mean of all 50 values near 111,111g.

To me, this looks like a classic null trend, suggesting there’s enough variance in the crop sell values to make any value near 111,111g approximately equally likely. So hitting 111,111g is pretty unlikely, but hitting either 1111111, 111110, 111100, 111000, 110000 is reasonably likely (about 5%). It matters what we perceive to be a lucky gold value! The approximately even spread in gold outcomes also suggests that the specific playstyle we choose doesn’t matter much, as long as it has a diverse set of sell values and only a few items are sold at a time.

Is there an analytic solution to this problem? I have no idea. One of the great things about simulations is that we can get an approximate answer even when we don’t know how to compute a probability analytically. There are many interesting related questions we could answer by slightly tweaking our simulation. For example, what if we sell crops in batches rather than one at a time? (Intuitively, this should decrease the odds… but will it?)

I encourage you to investigate these and similar questions yourself! The code for this post can be found on GitHub.